Question

You invest $1000 in an account that has an annual interest rate of 4%, compounded quarterly for 12 years. How much money will you have after the 12 years? $3138.43 O $3237.27 O $1601.03 O $1612.23

Answer 1

The compound interest formula is given by

`A=P(1+(r)/(n))^(n* t)`

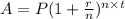
where A is the resulting amount after t years, P is the present value (or principal amount) , r is the annual interest rate and n is the number of compounding periods per year.

From the given information, we have that

`\begin{gathered} P=1000 \\ r=0.04 \\ n=4\text{ (quaterly=4 times per year)} \\ t=12\text{ years} \end{gathered}`

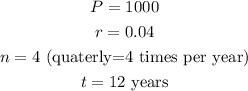
By substituting these values into the formula, we have

`A=1000(1+(0.04)/(4))^(4*12)`

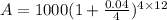
which gives

`\begin{gathered} A=1000(1.01)^(48) \\ A=1000(1.6122) \\ A=1612.226 \end{gathered}`

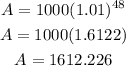
Therefore, by rounding to the nearest thousandth, the answer is $1612.23, which corresponds to the last option.