Question

A mail order company has a 6% success rate. If it mails advertisements to 538 people, find the probability of getting less than 28 sales. Round z-value calculations to 2 decimal places and final answer to at least 4 decimal places.

Answer 1

- This is a binomial probability problem because we have multiple trials.

- The formula for calculating the Z-value is:

`\begin{gathered} Z=(X-\mu)/(\sigma) \\ where, \\ \mu=\text{ The mean} \\ \sigma=\text{ The standard deviation} \\ X=\text{ The value we are testing} \end{gathered}`

- This value of Z can be used to calculate the probability we need using a Z-score calculator or a Z-distribution table.

- Before we proceed, we need to find the mean and the standard deviation as follows:

`\begin{gathered} \mu=np \\ n=\text{ Number of subjects} \\ p=\text{ The probability of success} \\ \\ \mu=(6)/(100)*538 \\ \\ \mu=32.28 \\ \\ \sigma=√(np(1-p)) \\ \sigma=\sqrt{538*(6)/(100)(1-(6)/(100))} \\ \\ \therefore\sigma=5.5085 \end{gathered}`

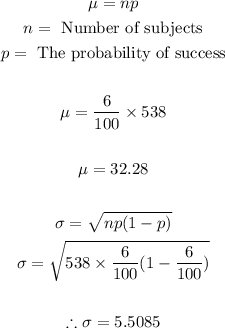
- Now that we have both the mean and the standard deviation, we can proceed to find the value of the Z-score as follows:

`\begin{gathered} Z=(X-\mu)/(\sigma) \\ \\ Z=(28-32.28)/(5.5085) \\ \\ \therefore Z=-0.78\text{ \lparen To 2 decimal places\rparen} \end{gathered}`

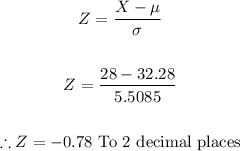
- Now that we have the Z-score value, we can proceed to find the corresponding probability for values less than X = 28 sales using a Z-distribution table or a Z-score calculator.

- Using a Z-score calculator, we have:

- Since we are looking for the probability of having sales lower than 28, we have:

[tex]P(X