Question

Solving a word problem with three unknowns using a linear... The sum of three numbers is 104. The first number is 6 less than the second. The third number is 3 times the second. What are the numbers?

Answer 1

`\begin{gathered} \text{First number=16} \\ \text{second number=22} \\ \text{Third number=66} \end{gathered}`

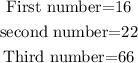
Step-by-step explanation:

Let the unknown numbers be x, y, and z where

• First number = x

,

• Second number = y

,

• Third number = z

If the sum of the three numbers is 104, then;

`x+y+z=104`

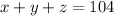
If the first number is 6 less than the second, hence;

`\begin{gathered} x=y-6 \\ \end{gathered}`

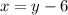
Also, if the third number is 3 times the second, then;

`z=3y`

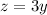
Substitute equations 2 and 3 into equation 1 to reduce the variables to the function of "y" only:

`\begin{gathered} x+y+z=104 \\ (y-6)+y+3y=104 \\ y-6+4y=104 \\ 5y-6=104 \\ 5y=104+6 \\ 5y=110\rbrack \\ y=(110)/(5) \\ y=22 \end{gathered}`

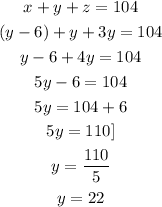
Get the first number "x"

`\begin{gathered} x=y-6 \\ x=22-6 \\ x=16 \end{gathered}`

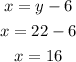
Get the third number "z"

`\begin{gathered} z=3y \\ z=3(22) \\ z=66 \end{gathered}`

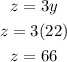
Therefore the three numbers are 16, 22, and 66.