Question

A normally distributed set of 250 values has amean of 88 and a standard deviation of 15.What percent of the values are expected tobe below 78?

Answer 1

We have a sample of size n=250. They are normally distributed with mean 88 and standard deviation of 15.

We have to find how many values from the sample are expected to be below 78.

We can calculate the z-score for 78 as:

`z=(X-\mu)/(\sigma)=(78-88)/(15)=-(10)/(15)=-(2)/(3)\approx-0.67`

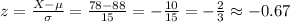
Then, we can calculate the percentage of values below 78 as the probability P(z<-0.67):

`P(X<78)=P(z<-0.67)=0.25249\approx25\%`

This percentage is independent of the sample size: it is the same percentage for 100 numbers, 250 numbers or 1000 numbers.

For 250, 63 numbers are expected to be below 78, as 0.25*250=63 approximately.

Answer: 25%