SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given points
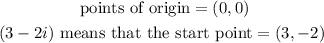
STEP 2: Write the formula for finding the modulus
![\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ \text{where (}x_(1,)y_1_{})=(0,0) \\ (x_2,y_2)=(3,-2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/r44kve2m0v1os77g6i05zn67744n0v4htp.png)
STEP 3: Substitute the values into the formula to get the answer
![\begin{gathered} d=\sqrt[]{(3-0)^2+(-2-0)^2} \\ d=\sqrt[]{(3)^2+(-2)^2} \\ d=\sqrt[]{9+4} \\ d=\sqrt[]{13} \\ d=3.605551275 \\ d\approx3.6\text{ to the nearest tenth} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nmh1aq56dimqslh9zzuuiimd84n5rpj0v1.png)
Hence, the required modulus is approximately 3.6 to the nearest tenth.