Question

Write an equation for each line.9р87n3215689-9-8-2-6 -5 -3-2 -1 0-1-2-3-4-5m-6-7-8-9No

Answer 1

Answers:

line l: y = 4

line m: y = -2x + 4

line n: y = x - 1

line p: x = -4

Step-by-step explanation:

To find the equation of a line we can use the following:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

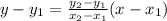
Where (x1, y1) and (x2, y2) are two points in the line.

So, to find the equation for line l, we need to identify 2 points in the line. So, these points can be (1, 4) and (2, 4). So, replacing (x1, y1) by (1, 4) and (x2, y2) by (2, 4), we get that the equation of the line l is:

`\begin{gathered} y-4=(4-4)/(2-1)(x-1) \\ y-4=(0)/(2)(x-1) \\ y-4=0(x-1) \\ y-4=0 \\ y=4 \end{gathered}`

Therefore, the equation of line l is y = 4

In the same way, the equation of the black line m can be calculated replacing (x1, y1) by (2, 0) and (x2, y2) by (0, 4). So, the equation of the line m is:

`\begin{gathered} y-0=(4-0)/(0-2)(x-2) \\ y=(4)/(-2)(x-2) \\ y=-2(x-2) \\ y=-2x+4 \end{gathered}`

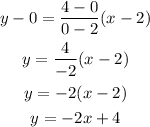
Therefore, the equation of line m is y = -2x + 4

So, the equation of the green line n can be calculated using the points (1, 0) and (3,2). Then, replacing (x1, y1) by (1, 0) and (x2, y2) by (3, 2), we get:

`\begin{gathered} y-0=(2-0)/(3-1)(x-1) \\ y=(2)/(2)(x-1) \\ y=1(x-1) \\ y=x-1 \end{gathered}`

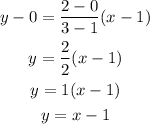
Therefore, the equation of line n is y = x - 1

Finally, to calculate the equation of line p, we can't use the equation above, so we need to know that the vertical lines have equations with the form:

x = contact.

Since the vertical line is located at x = -4, the equation of the line p is x = -4