Question

Given two angles that measure 50° and 80° and a side that measures 4 feet, how many triangles, if any, can be constructed?

Answer 1

Remember that the sum of the three interior angles of a triangle is 180°.

Now, let's call the remaining angle x. We would have:

`x+50+80=180`

Solving for x,

`\begin{gathered} x=180-50-80 \\ \Rightarrow x=50 \end{gathered}`

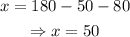
From this, we get that the remaining anlge has to measure 50°. Now, as we already have a side that measures 4 feet, the other two sides are constrained; neither of them can have any measurement that's different to the one that constructs the remaining 50° angle.

Therefore, only one triangle can be constructed.