The formula for the value of discriminant in a quadratic equation in the form ax^2 + bx + c = 0 is :
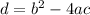
Where d is the discriminant and
a, b, c are the coefficients in the quadratic equation.
From the given problem,
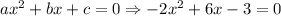
a = -2, b = 6 and c = -3
Using the formula above,
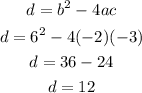
Note that if the discriminant is greater than 0, the number of real solution is 2.
The answer is
discriminant = 12
Number of real solutions = 2