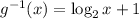Question

Please just answer part B And please explain every step and how its simplified so I can understand better.

Answer 1

Given that

We have to find the inverse of a function and the function is

`g(x)=2^(x-1)`

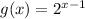
Explanation -

The steps to find the solution are -

(1). First, we will consider the function equal to y as

`\begin{gathered} g(x)=y \\ x=g^(-1)(y)----------(i) \\ y=2^(x-1) \end{gathered}`

(2). Now from this, we will find the value of x in terms of y.

And we will take the base of the log as 2 because the x is in the power of 2. As an exponential function.

As

`\begin{gathered} y=(2^x)/(2) \\ Taking\text{ the }\log_2\text{ on both sides we have} \\ \log_2y=\log_2((2^x)/(2)) \\ \log_2y=\log_22^x-\log_22 \\ \\ Using\text{ the formulae of log,} \\ \begin{equation*} \log_a((b)/(c))=\log_ab-\log_ac \end{equation*} \\ \log_aa^p=p*\log_aa \\ and\text{ }\log_aa=1 \\ \\ Now,\text{ } \\ \log_2y=\log_22^x-1 \\ \log_2y=x\log_22-1 \\ \log_2y=x-1 \\ x=\log_2y+1 \end{gathered}`

(3). Now from eq (i) we have

`g^(-1)(y)=\log_2y+1`

(4). At last, we will replace y with x. Then,

`g^(-1)(x)=\log_2x+1`

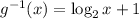
Final answer -

The final answer is
`g^(-1)(x)=\log_2x+1`