Answer
Step-by-step explanation
Mathematically, if a point R(x, y) divides the coordinates S (x₁, y₁) and T (x₂, y₂) internally in the ratio m:n then point R(x, y) is given as
x = [(mx₂ + nx₁)/(m + n)]
y = [(my₂ + ny₁)/(m + n)]
For this question, we are given that
R (x, y) = R(-2, -1)
S (x₁, y₁) = S (-14, 3)
T (x₂, y₂) = ?
Since it is divided equally into two parts (As per the midpoint), m : n = 1 : 1
x = -2
y = -1
x₁ = -14
y₁ = 3
x₂ = ?
y₂ = ?
m = 1
n = 1
x = [(mx₂ + nx₁)/(m + n)]
-2 = [(1 × x₂) + (1 × -14)]/(1 + 1)
-2 = [x₂ - 14]/2
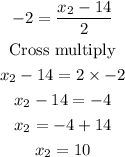
y = [(my₂ + ny₁)/(m + n)]
-1 = {