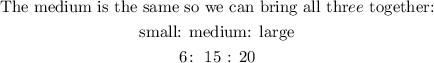Question

A café has three different sizes of plate. The ratio of small to medium is 2:5 and the ratio of medium to large is 3:4What is the ratio of small plates, to medium plates to large plates?

Answer 1

6: 15 : 20

Step-by-step explanation:

Ratio of small to medium = 2 : 5

Ratio of medium to large = 3 : 4

We need to make the medium in both ratios equivalent since medium is common to both:

`\begin{gathered} \frac{small}{\text{medium}}\text{ = }(2)/(5) \\ \frac{medium}{\text{large}}=(3)/(4) \\ \text{for medium to be equivalent, we multiply ratio by 3} \\ we\text{ multiply the second ratio by 5} \\ \text{LCM = 3}*5\text{ = 15} \end{gathered}`

We multiply the numerator by same amount we multiply the denuominator in both ratios:

`\begin{gathered} \frac{small}{\text{medium}}\text{ = }(2)/(5)*(3)/(3)\text{ } \\ \frac{small}{\text{medium}}=\text{ }(6)/(15) \\ \\ \frac{medium}{\text{large}}=(3)/(4)*(5)/(5) \\ \frac{medium}{\text{large}}=\text{ }(15)/(20) \end{gathered}`

The ratio of small to medium to large:

`\begin{gathered} \text{The medium is the same so we can bring all thr}ee\text{ together:} \\ \text{small: medium: large} \\ 6\colon\text{ 15 : 20} \end{gathered}`