Answer:
x = 25
scalene, acute
Explanation:
Sum of the interior angles of a triangle = 180°
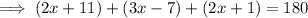
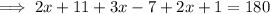
Collect like terms:
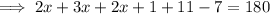
Combine like terms:
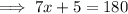
Subtract 5 from both sides:
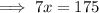
Divide both sides by 7:
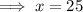
Substituting found value of
 into the three angle expressions:
into the three angle expressions:
∠A = (2 x 25) + 11 = 61°
∠B = (3 x 25) - 7 = 68°
∠C = (2 x 25) + 1 = 51°
This is a scalene triangle as it has three different angles and three different side lengths (non-congruent).
It is also an acute triangle as all interior angles are less than 90°