Answer:
To find the perimeter of the regular pentagon.
O is the center of the regular pentagon from the figure.
we know that, There are 360 degrees around a point, the angle formed over each side are equal that is eual to 360/5 =72
In the triangle made by the side and line joinging center, we get
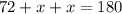
whereb x is the angle made by the line joining to the center and one of the side.we get,
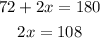
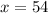
Consider the right angled triangle,
we know that,
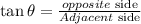
we get,
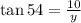
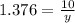
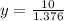
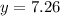
Side of a pentagon (s)= 2x7.26=14.52
Perimeter of a pentagon is,
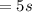
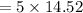
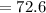
Perimeter of a pentagon is 72.6 units.