Suppose that the corrals are rectangular in shape. The formula of the area of a rectangle is
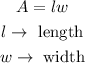
Therefore, the areas of the four different corrals are
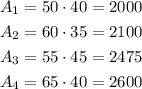
Then, divide each area by its corresponding population,
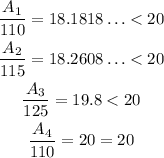
Therefore, the only corral that meets the requirement is corral 4, the answer is option D.