Answer:
The rate of change of elevation tends to a constant value.
Step-by-step explanation:
The average rate of change of e(x) on the interval [a, b] defined as
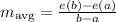
which explicitly we can write as
![m_{\text{avg}}=\frac{\sqrt[]{b-10}-\sqrt[]{a-10}}{b-a}](https://img.qammunity.org/2023/formulas/mathematics/college/24lug0czbs9vwwl2ap4pmqsxzfpxsahfcw.png)
Now, the question is, what happens to m_avg as we increase b while keeping a fixed?
As b becomes large then √b -10 becomes √b and b - a becomes b (since a is comparatively small); therefore, m_avg becomes
![m_{\text{avg}}=\frac{\sqrt[]{b-10}-\sqrt[]{a-10}}{b-a}\Rightarrow\frac{\sqrt[]{b}-\sqrt[]{a-10}}{b}\Rightarrow\frac{\sqrt[]{b}}{b}](https://img.qammunity.org/2023/formulas/mathematics/college/enekg95g1w10l66hv49mita7tcn0beyv0i.png)
![\Rightarrow m_{\text{avg}}=\frac{\sqrt[]{b}}{b}](https://img.qammunity.org/2023/formulas/mathematics/college/9ngz408vmmn2uen6igx9mpkm3vgi2fgsk1.png)
which for any fixed value of b is a constant.
The same behaviour can be extrapolated by looking at the graph of e(x).
As can be seen from the graph, as x increases, the slope of the function becomes flatter and flatter, meaning it tends to be a constant. In other words, for large values of x, you can approximate the slope of the function by a straight line.