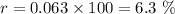Question

Given the following exponential function, identify whether the change represents growth or decay, and determine the percentage rate of increase or decrease. y = 3900(0.937)

Answer 1

This function represents a decay. The rate of decrease is 6.3%

Step-by-step explanation

When the growth/decay factor is less than 1, the function represents a decay:

`y=a(b)^x`

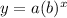
b is the growth/decay factor.

For a function that represents decay, the decrease factor is:

`b=1-r`

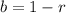
where r is the rate of decrease. In this case, b = 0.937. We can find r:

`\begin{gathered} 0.937=1-r \\ r=1-0.937 \\ r=0.063 \end{gathered}`

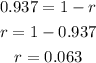
To know the rate as a percentage, we have to multiply it by 100:

`r=0.063*100=6.3\text{ \%}`