Question

A 7.00 ✕ 105 kg subway train is brought to a stop from a speed of 0.500 m/s in 0.800 m by a large spring bumper at the end of its track. What is the force constant k of the spring? N/m

Answer 1

Given:

The mass of the subway train is: m = 7 × 10⁵ kg

The speed of the train is: v = 0.5 m/s

The train stops by covering 0.8 m of distance by the spring bumper. Thus, x = 0.8 m

To find:

The force constant of the spring.

Step-by-step explanation:

The moving train is stopped by the spring bumper this means that the kinetic energy of the moving is stored as the elastic potential energy of the spring. Thus,

Kinetic Energy of Train = Elastic Potential Energy of Spring

The kinetic energy of the train is given as:

`KE=(1)/(2)mv^2`

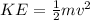
The elastic potential energy of the train is given as:

`PE=(1)/(2)kx^2`

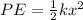
Here, k is the spring constant or force constant.

Equating KE and PE, we get:

`\begin{gathered} (1)/(2)mv^2=(1)/(2)kx^2 \\ \\ mv^2=kx^2 \\ \\ k=(mv^2)/(x^2) \end{gathered}`

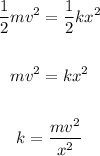
Substituting the values in the above equation, we get:

`\begin{gathered} k=\frac{7*10^5\text{ kg}*(0.5\text{ m/s\rparen}^2}{(0.8\text{ m\rparen}^2} \\ \\ k=\frac{7*10^5\text{ kg}*0.25\text{ m}^2\text{/s}^2}{0.64\text{ m}^2} \\ \\ k=273437.5\text{ N/m} \end{gathered}`

Final answer:

Thus, the force constant of the spring is 273437.5 N/m.