ANSWER :
D.
EXPLANATION :
From the problem, we have a graph that goes to positive infinity as x goes to the positive infinity.
Note that in an exponential function :

The function goes to positive infinity if "a" is greater than 1
The function goes to negative infinity if "a" is less than 1
Since the given graph goes to positive infinity, we are looking for the function whose "a" is greater than 1.
We have Options A and D.
Next is to check the y-intercept.
The graph intersects the y-axis at (0, -3)
Substitute x = 0 and f(x) should be -3
For Option A :
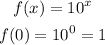
For Option D :
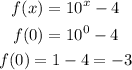
Therefore, the answer is D.