Question

What is an equation of the line that passes through the point (-3,-5) and isparallel to the line 25 + 3y = 15?

Answer 1

We have to find the equation of a line that pass through the point (-3,5) and is parallel to the line 25x+3y=15.

All parallel lines to 25x+3y=15 can be written as:

`25x+3y=C`

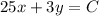
where C is a constant that allows us to change the position of the line to fit any point.

As the point (-3,5) belongs to the line we are looking for, it has to satisfy the equation. So we can write:

`\begin{gathered} 25x+3y=C \\ 25(-3)+3(5)=C \\ -75+15=C \\ C=-60 \end{gathered}`

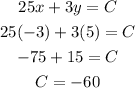
With the value of C defined, we can write the equation of the line as:

`25x+3y=-60`

Answer: 25x+3y=-60