Question

I need help answering this please ! The calculator has to be In degree mode and the second picture is used to help you find the answer

Answer 1

A) AB is a side and not an angle. A side is a length, an angle is a junction of two lines.

B) You are given a side, AC and two angles, Angles B and C

C) Angles and lines are named according to their oppositeness. Angle A is opposite to side a.

`(\sin A)/(BC)=(\sin B)/(AC)=(\sin C)/(AB)=(\sin A)/(BC)=(\sin50)/(12)=(\sin 62)/(AB)`

D) To find AB, we crossmultiply with the expression in the middle of the equation. This gives:

`AB\text{ = }\frac{\text{12 sin 62}}{\sin 50}=13.8313`

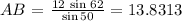
Line AB is 13.83 to the nearest hundredth