Question

determine the equation of the ellipse with center (2,2), focus (2,0), and vertex (2,5).multiple choices

Answer 1

Given:

The ellipse has center (2,2), focus (2,0), and vertex (2,5).

The equation of elllipse is given as,

`((x-h)^2)/(b^2)+((y-k)^2)/(a^2)=1`

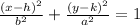
a is the distance between vertex and center.

`\begin{gathered} a=\sqrt[]{(2-2)^2+(5-2)^2} \\ a=\sqrt[]{3^2}=3 \end{gathered}`

c is distance between focus and center.

`\begin{gathered} c=\sqrt[]{(2-2)^2+(0-2)^2} \\ c=\sqrt[]{4} \\ c=2 \end{gathered}`

It gives,

`\begin{gathered} c^2=a^2-b^2 \\ 2^2=a^2-b^2 \\ b^2=9-4 \\ b^2=5 \\ b=\pm\sqrt[]{5} \\ b=\sqrt[]{5}\ldots\ldots\text{ Since b is distance and it should be positive} \end{gathered}`

So, the equation of the ellipse is,

`\begin{gathered} ((x-h)^2)/(b^2)+((y-k)^2)/(a^2)^{}=1 \\ \frac{(x-2)^2}{(\sqrt[]{5})^2^{}}+((y-2)^2)/(3^2)=1 \\ \frac{(x-2)^2}{5^{}}+\frac{(y-2)^2}{9^{}}=1 \end{gathered}`

Answer: option b)