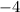For the function f(x) to be greater than 0 (f(x) > 0), we need to identify those regions strictly above the x-axis.
From the graph, these regions are (in interval notation):
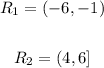
For each region there is an inequality:
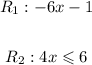
The domain is the set of x-values the function takes. Then, from the graph, we can see that the function is defined from x = -7 to x = 6. The domain of f(x) is:

The range is the set of y-values the function takes. From the graph, we see that the function has a minimum of -8 and a maximum of 12. Then, the range is:
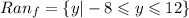
For the x-intercepts (points with y = 0), we have:
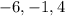
For the y-intercept (the point with x = 0):