ANSWER
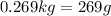
Step-by-step explanation
Parameters given:
Mass of glass, mg = 0.6 kg
Mass of ice tea, mt = 1.2 kg
Temperature of tea and glass = Tg = Tt = T1 = 19°C
Required temperature, T2 = 1°C
Temperature of ice, Ti = -15°C
The sum of the heat lost by the glass and the heat lost by the tea must be equal to the heat gained by the ice:
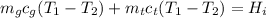
where cg = specific heat of the cup.
ct = specific heat capacity of the tea
Hi = heat gained by ice
The heat gained by ice is given as the sum of the heat gained to convert the ice to ice at 0°C, the heat gained to convert the ice at 0°C to water at 0°C and the heat gained to convert water at 0°C to water at 1°C:
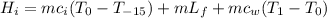
where ci = specific heat capacity of ice
Lf = latent heat of fusion of ice
Therefore, we can substitute this into the original formula:
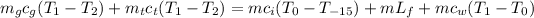
Solving for m in the equation above, the mass of ice needed is:
![\begin{gathered} (0.6*837*(19-1))+(1.2*4186*(19-1))=(m*2090*(0-(-15)))+(m*33400)+(m*4186*(1-0)) \\ \\ 9039.6+90417.6=31350m+334000m+4186m \\ \\ 99457.2=369536m \\ \\ m=(99457.2)/(369536) \\ \\ m=0.269kg=269g \end{gathered}]()
That is the mass of ice needed.