Question

Which are the foci of the hyperbola represented by… Thanks!

Answer 1

The equation is given to be:

`x^2-3y^2+12=0`

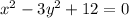
We can write the equation in the standard form of the equation of a hyperbola to be:

`(\left(y-0\right)^2)/(2^2)-(\left(x-0\right)^2)/(\left(2√(3)\right)^2)=1`

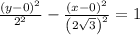
Therefore, we have the following parameters:

`\left(h,\:k\right)=\left(0,\:0\right),\:a=2,\:b=2√(3)`

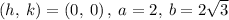
Recall the hyperbola foci definition:

Therefore, the value of c will be:

`\begin{gathered} c=\sqrt{2^2+(2√(3))^2} \\ c=4 \end{gathered}`

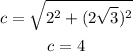
Therefore, the foci will be:

`\begin{gathered} \left(h,\:k+c\right),\:\left(h,\:k-c\right)=\left(0,\:0+4\right),\:\left(0,\:0-4\right) \\ Foci=\left(0,\:4\right),\:\left(0,\:-4\right) \end{gathered}`

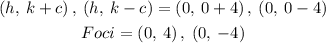
The correct option is the FIRST OPTION.