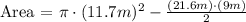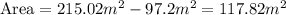Question

6.25 ft7.14 am25 cm11 am8.9 m21.6 m

Answer 1

For figure 6

In figure 6 we have a circle and a rectangle. The shaded area will be the difference between the area of the rectangle of side 25ft and the area of the ciercle of diameter 25ft.

The radius of the circle will be 25ft/2 = 12.5ft

Then, the area will be:

`\begin{gathered} \text{Area}=(25ft)\cdot(25ft)-\pi\cdot(12.5ft) \\ \text{Area}=625ft^2-490.87ft^2=134.13ft^2 \end{gathered}`

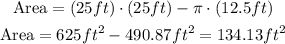
For figure 7

In figure 7 we have a rectangle and a triangle. The shaded area will be the area of the rectangle minus the area of the triangle. The sides of the triange are 25cm and 14cm, while the triangle has a base of 25cm and a height of 11cm. We can say 11cm is the height because according to the figure this height forms a right triangle with the base.

Then, the area will be:

Area = 350cm^2 - 137.5cm^2

Area = 212.15cm^2

For figure 8

The figure 8 has a triangle and a semicircle. The shaded area will be the difference between the area of the semicircle and the area of the triangle.

We can say this is a righ triangle because his hypotenuse is the diameter of a circle and the hycks join in the circumference.

The hypotenuse is calculated with hicks 9m and 21.6m

`h=\sqrt[]{(9m)^2+(21.6m)^2}=\sqrt[]{81m^2+466.56m^2}=\sqrt[]{547.56m^2}=23.4m`

The area of the triangle could be calculated with the base 21.6m and the height 9m., and the area of the semicircle could be calculated considering his radius as the half of diameter: 23.4/2 = 11.7m

Then the area will be:

`\text{Area = }\pi\cdot(11.7m)^2-((21.6m)\cdot(9m))/(2)`
`\text{Area}=215.02m^2-97.2m^2=117.82m^2`