Question

The mole fraction of iron(II) bromide, FeBr2, in an aqueous solution is 6.15×10-2. The percent by mass of iron(II) bromide in the solution is what %?

Answer 1

First, let's put the info into symbols:

`\begin{gathered} X_(FeBr_2)=\text{ 6.15*10}^(-2) \\ \end{gathered}`

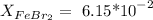
As the mole fractions have to add up to 1, we can calculate the water mole fraction, substracting:

`X_(H_2O)=\text{ 1-6.15*10}^(-2)=0.9385`

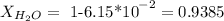
If we make the supposition that we have 1 mole of the solution, we would have the next quantities of each substance:

`6.15*10^(-2)\text{ moles of FeBr}_2\text{ and 0.9385 moles of water. }`

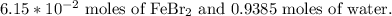
Now, we can convert these moles into mass through the molecular weight of each substance:

`\begin{gathered} M.W\text{ of water: 2*1+16=18 g/mole} \\ M.W.\text{ of iron \lparen II\rparen bromide: 56+80*2=216 g/mole} \\ \\ 6.15*10^(-2)moles\text{ FeBr}_2*\frac{216\text{ g}}{1\text{ mole}}=\text{ 13.284 g FeBr}_2 \\ \\ 0.9385\text{ moles H}_2O\text{ * }\frac{18\text{ g}}{1\text{ mole}}=16.893\text{ g H}_2O \end{gathered}`

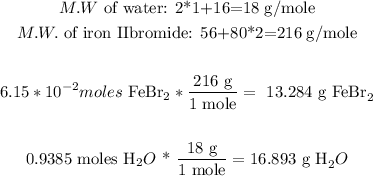
Now, we can calculate the mass percentage, because we have the mass of the substrate and the mass of the solution (the addition of water and iron (II) bromide):

`\%\text{ m/m FeBr}_2=\frac{13.284\text{ g}}{13.284g+16.893g}*100=44.020\text{ \% m/m}`

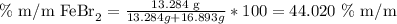
The answer is that the %m/m of iron bromide in the solution is 44.020%