Question

A phone company has a monthly cellular plan where a customer pays a flat monthly fee and then a certain amount of money per minute used on the phone. If a customer uses 410 minutes, the monthly cost will be $71.50. If the customer uses 720 minutes, the monthly cost will be $118.Find a linear equation for the monthly cost of the cell plan as a function of x, the number of monthly minutes used. Type your answer in slope intercept form (y=mx+b) without any spaces between the characters. The function is C(x)=AnswerUse your equation to find the total monthly cost if 687 minutes are used. The cost will be $Answer

Answer 1

The cost for 410 minutes is $71.50 and cost for 720 minutes is $118.

Determine the equation for (410,71.50) and (720,118).

`\begin{gathered} y-71.50=(118-71.50)/(720-410)(x-410) \\ y-71.50=(46.5)/(310)(x-410) \\ y=0.15(x-410)+71.50 \\ y=0.15x-61.5+71.50 \\ =0.15x+10 \end{gathered}`

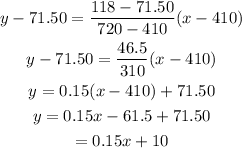
So function is C(x) = 0.15x + 10.

Substitute 687 for x in equation to determine the cost for 687 minutes.

`\begin{gathered} C(687)=0.15\cdot687+10 \\ =103.05+10 \\ =113.05 \end{gathered}`

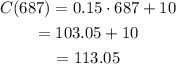
So monthly cost if 687 minutes used is 113.05.