C) 6√2
1) Examining this triangle, we can conclude this is a right triangle and state that we can find the missing side (the adjacent leg) to angle 45º using the following trigonometric ratio Cosine:
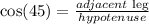
2) So we can plug into that the given values for those legs:
![\begin{gathered} \cos \text{ (45)=}(x)/(12) \\ \frac{\sqrt[]{2}}{2}=(x)/(12) \\ \\ 2x=12\sqrt[]{2} \\ (2x)/(12)=\frac{12\sqrt[]{2}}{12} \\ (x)/(6)=\sqrt[]{2}\text{ x 6} \\ x=6\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6eu6cywadznkcvzgpvhsq5kt143enti8h7.png)
Note that we cross multiplied those ratios, and divided them by 12. Finally, to get rid of the fraction x/6 we multiplied that by 6 on both sides.
3) Hence, the answer is 6√2