Question

Table 1 shows two variables m and n that are related by an equation n ab^m where a and b are constantBelow shows table 1:m : 1 2 3 4 5n : 24 48 96 192 384a) plot the graph of log10 n against m by using a scale of 2 cm to 1 unit on the x-axis and 2cm to 1.2 unit on the y-axisb) hence, find the value of a and b

Answer 1

a) The plotted graph is shown in the Explanation below.

b) a = 12, b = 2

Step-by-step explanation

n = a(b^m)

Taking the logarithm of both sides

log n = log [a(b^m)]

log n = log a + log (b^m)

log n = log a + m log b

So, to first plot the graph, we know we need to rewrite this equation to match the equation of a straight line. Equation of a straight line is

y = mx + b

where

y = y-coordinate of a point on the line.

m = slope of the line.

x = x-coordinate of the point on the line whose y-coordinate is y.

b = y-intercept of the line.

log n = (log b) m + log a

y = mx + b

y-axis = log n

slope = log b

x-axis = m

intercept = log a

So, we need to plot log n (on the y-axis) against m (on the x-axis)

m | n | log n

1 | 24 | 1.38

2 | 48 | 1.68

3 | 96 | 1.98

4 | 192 | 2.28

5 | 384 | 2.58

The values for log n are then plotted against the corresponding value of m

The image is presented below.

From the graph, we can easily see that

Intercept = 1

To obtain the slope, for a straight line, the slope of the line can be obtained when the coordinates of two points on the line are known. If the coordinates are (x₁, y₁) and (x₂, y₂), the slope is given as

Using the two farthest points,

(x₁, y₁) and (x₂, y₂) = (1, 1.38) and (5, 2.58)

`\begin{gathered} Slope=m=\frac{Change\text{ in y}}{Change\text{ in x}}=(y_2-y_1)/(x_2-x_1) \\ \text{Slope = }(2.58-1.38)/(5-1)=(1.2)/(4)=0.3 \end{gathered}`

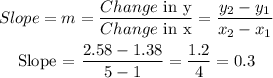
b) Intercept = log a = 1.08

a = log⁻¹ (1.08) = 12

Slope = log b = 0.3

b = log⁻¹ (0.3) = 1.995 = 2

n = 12 (2^m)

We can test this by putting values of m in the expression looking to get n

when m = 1,

n = 12 (2^1)

n = 12 (2) = 24

when m = 5

n = 12 (2^5)

n = 12 (32) = 384

So, our model works!!!

Hope this Helps!!!