Question

Prove the segments joining the midpoint if consecutive sides of an isosceles trapezoid form a rhombus.

Answer 1

DEFG is a rhombus by definition of rhombus (option B)

Step-by-step explanation:

To prove that DEFG is a rhombus, we will find the distance between all the 4 sides of the quadrilateral. A rhombus has all 4 sides equal.

Distance formula is given as:

`$$dis\tan ce\text{ = }\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2}$$`
`\begin{gathered} distance\text{ DE: D}(-a-b,\text{ c})\text{ and E}(0,\text{ 2c}) \\ x_1=-a-b,y_1=c,x_2=0,y_2\text{ = 2c} \\ distance\text{ DE = }\sqrt{(0\text{ - }(-a-b))^2\text{ + }(2c\text{ - c})^2} \\ distance\text{ DE = }\sqrt{(0\text{ +}a+b)^2\text{ + c}^2}\text{ } \\ distance\text{ DE = }\sqrt{(\text{a + b})^2+c^2} \end{gathered}`
`\begin{gathered} distance\text{ EF: E}(0,\text{ 2c})\text{ and F}(a\text{ + b, c}) \\ x_1=0,y_1=2c,x_2=a+b,y_2\text{ = c} \\ distance\text{ EF = }\sqrt{(c\text{ - 2c})^2+\text{ }(a\text{ + b - 0})^2} \\ distance\text{ EF = }√((-c)^2+(a+b)^2)\text{ } \\ \text{distance EF = }\sqrt{c^2\text{ + }(a+b)^2} \end{gathered}`
`\begin{gathered} distance\text{ GF: G}(0,\text{ 0})\text{ and F }(a+b,\text{ c}) \\ x_1=0,y_1=0,x_2=a+b,y_2\text{ = c} \\ distance\text{ GF = }\sqrt{(c\text{ - 0})^2+\left(a+b-0\right)^2} \\ distance\text{ GF = }√(c^2+(a+b)^2) \end{gathered}`
`\begin{gathered} distance\text{ DG: D}(-a-b,\text{ c})\text{ and G }(0,\text{ 0}) \\ x_1=-a-b,y_1=c,x_2=0,y_2\text{ = 0} \\ distance\text{ GD = }√((0-c)^2+(0-(-a-b))^2) \\ distance\text{ GD = }√((-c)^2+\left(0+a+b\right)^2) \\ distance\text{ GD = }\sqrt{c^2\text{ + }(a+b)^2} \end{gathered}`

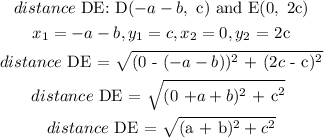
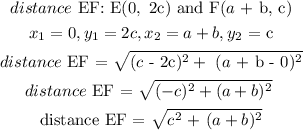
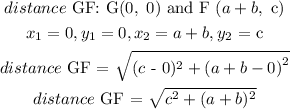
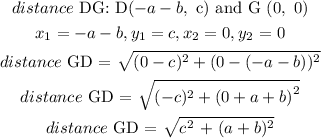
From our calculation, Distance DE = Distance EF = Distance GF = Distance GD

All 4 sides are equal (congruent)

DEFG is a parallelogram with congruent sides. So DEFG is a rhombus by definition of rhombus (option B)