Question

Identify the slope and y-intercept of the linear equation then graphY = -2x/7 + 2Y = -5x/6 - 18

Answer 1

For this problem, we are given a certain system of equations and we need to identify the slope, y-intercept and trace the graphs for the system.

The system is given below:

`\begin{cases}y={-(2x)/(7)}+2 \\ y=-{(5x)/(6)}-18\end{cases}`

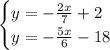
Both equations are in the slope-intercept form, which means that the slope is the number multiplying "x" and the intercept is the number isolated.

For equation 1:

`\begin{gathered} \text{ slope}=(-2)/(7)\\ \\ \text{ intercept}=2 \\ \end{gathered}`

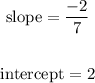
For equation 2:

`\begin{gathered} \text{ slope}=(-5)/(6) \\ \text{ intercept}=-18 \end{gathered}`

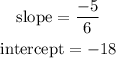
The slope is the increase on the graph that the y-axis has for each 1 unit increase in the x-axis. This means that from x = 0 to x = 1 the first equation will decrease 2/7 units and the second equation will decrease 5/6 units. The y-intercept is the point at which the function crosses the y-axis.

With this we can create the graphs: