Question

Which values are solutions to the inequality below?Check all that apply.√x ≤ 11choices: 121, 120, 111, -10, 122, no solution

Answer 1

Consider the given inequality,

`\sqrt[]{x}\leq11`

Note that a square root inequality is defined only if the 'x' is non-negative.

`x\ge0`

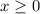
Now, squaring both sides will not affect the inequality as both sides are positive terms,

`\begin{gathered} (\sqrt[]{x})^2\leq11^2 \\ x\leq121 \end{gathered}`

Combining the two results,

`0\leq x\leq121`

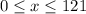
Thus, the solution set to the inequality is the set of all real numbers from 0 to 121 .