The Solution:
Given:
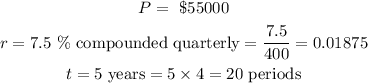
Required:
Find the value of the investment after 5 years.
The Formula:
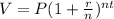
In this case,
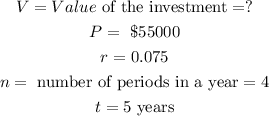
Substitute:
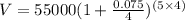
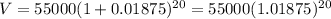

Answer:
(a) $79,747.14
Find the number of months it will take the account to increase to more than $70,000
Solve for n in the equation below:

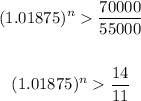
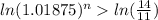

Answer:
13 months or more