Question

Hello I need help in understanding a problem! Thank you!

Answer 1

The question asks us to find the vertex of the equation below:

`y=-0.017x^2+1.08x+5.8`

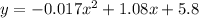
The question asks us to find the vertex using two methods.

For the first method, we will use is to plot the graph of the equation and highlight the coordinate of the vertex on the graph.

The second method will employ completing the square method to find the vertex of the equation.

Method 1:

Plotting the graph of the equation, we have:

From the plot above, we can see that the vertex is: (31.765, 22.953)

The next method must get the same values for the vertex coordinates.

Method 2:

This method is the completing the square method. It converts quadratic equations into their vertex forms.

The general equation for a vertex form of a quadratic equation is:

`\begin{gathered} y=(x-h)^2+k \\ \text{where} \\ (h,k)\to\text{ Vertex coordinates} \end{gathered}`

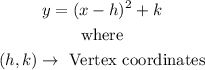
In order to apply "completing the square" method, we need to complete the following steps:

1. Factor out the coefficient of x-squared

2. Divide the coefficient of x by 2 and square the result

3. Add and subtract the answer from step 2 to the equation; then factorize to get the quadratic equation

in its vertex form.

Now, let us proceed to find this vertex form:

`y=-0.017x^2+1.08x+5.8`

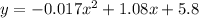
1. Factor out the coefficient of x-squared

`\begin{gathered} y=-0.017(x^2+(1.08)/(-0.017)x)+5.8 \\ y=-0.017(x^2-63.5294x)+5.8 \end{gathered}`

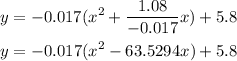
2. Divide the coefficient of x by 2 and square the result

`\begin{gathered} \text{Coefficient of x is: -63.5294} \\ \text{Divide the coefficient by 2 = }(-63.5294)/(2)=-31.7647 \\ \\ \text{square the result = }(-31.7647)^2=1008.996 \end{gathered}`

3. Add and subtract the answer from step 2 to the equation; then factorize to get the quadratic equation

in its vertex form.

`\begin{gathered} y=-0.017(x^2-63.5294x)+5.8 \\ \text{Add and subtract 1008.996} \\ y=-0.017(x^2-63.5294x+1008.996-1008.996)+5.8 \\ \text{remember that, 1008.996 =(31.7647})^2\text{ , from above} \\ \\ y=-0.017(x^2-63.5294x+31.7647^2-1008.996)+5.8 \\ y=-0.017(x^2-2(31.7647)x+31.7647^2-1008.996)+5.8 \\ \\ \text{Also, } \\ (x^2-2xb+b^2)=(x-b)^2 \\ if\text{ b = 31.7647,} \\ \\ y=-0.017((x-31.7647)^2-1008.996)+5.8 \\ \text{Expand the outer bracket} \\ \\ y=-0.017(x-31.7647)^2-0.017(-1008.996)+5.8 \\ y=-0.017(x-31.7647)^2+17.1529+5.8 \\ \\ y=-0.017(x-31.7647)^2+22.9529 \end{gathered}`

Now that we have the equation in vertex form, we just need to compare the equation with the general formula for the vertex form, to get the coordinates of the vertex.

`\begin{gathered} y=a(x-h)^2+k \\ y=-0.017(x-31.7647)^2+22.9529 \\ \text{ Comparing the two equations, we can conclude;} \\ \\ a=-0.017,h=31.7647,k=22.9529 \\ \\ \therefore\text{ vertex (h, k) = (31.7647, 22.9529)} \end{gathered}`

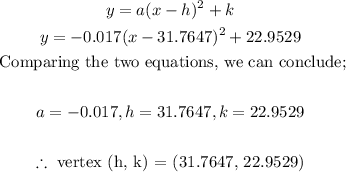
Therefore, the final answer is: (31.7647, 22.9529)