Question

A rectangular piece of cardboard that is 10 inches by 14 inches has squares of length x inches on a side cut from each corner. (Assume that 0 < x < 5.) If the flaps of the figure are folded up, an open box is formed. Represent the volume of this box in the form of a polynomial function V(x).

Answer 1

This is an aproximation of the described situation. We are taking 4 squares of side lenght x from each corner.

The dashed lines mark up what would be the base of the box. The blue scrabbled areas will be the sides of the box.

Recall that to calculate the volume of the box, we need to multiply the lenghts of each side of the base and then multiply it by the height of the box. So, to calculate the volume we need to determine the lenght of the dashed lined.

Let us calculate the lenght of the black dashed lines. Notice that the horizontal side has a total lenght of 14. So, since we are taking 2 squares of side x, we have that the lenght of the dashed line plus twice the lenght x, we get the total lenght of the side. That is

`\text{Black dashed line + 2x = 14}`

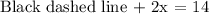
Then the lenght of the black dashed line is 14-2x.

In the same manner, we can calculate the red dashed lines' lenght. It is 10-2x. Now, our box would be

In the picture, the green line represents the height. Comparing the blue and red lines, we have that the lenght of the green line corresponds to the lenght of the side of the square (x).

So now, we know that the volume of the box is

height * lenght of the base * width of the base = (14-2x)*(10-2x) * (x)

which is a polynomial of the variable x.