To check whether the lines are perpendicular or parallel, we will use the following rules:
1) For parallel lines, the slopes are equal.
2) For perpendicular lines, the product of the slopes is equal to -1.
Slope of line AB:
Using
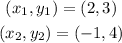
The slope is given as
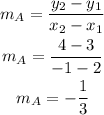
Slope of line CD:
Using
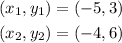
The slope is given as
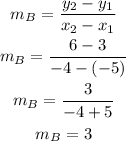
Comparing both slopes, we can observe that
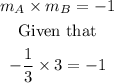
Therefore, both lines are PERPENDICULAR.