Question

Cannon wants to put as much as he can into a retirement account as soon as he starts working. He deposits $25,000 at then end of each year for 5 years in an account paying 6% interest compounded annually. How much will he have in the account at the start of the 6th year? A) $140,927.34 B) $174,382.96 C) $395,240 D) $557,593.99

Answer 1

The compound interest formula is given by the formula

`A\text{ = }p(1+(r)/(100))t`

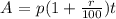
Where A = Amount after t years

r = rate = 6

t = time = 5

p = $ 25000

For the first year

`\begin{gathered} A=\text{ 25000(1+0.06)} \\ =25000*1.06=26500 \end{gathered}`

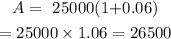
For the second year

P=26500+25000=51500

`\begin{gathered} A=51500(1+0.06) \\ =515000*1.06=54590 \end{gathered}`

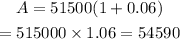
For the third year

P=54590 + 25000=79590

`\begin{gathered} A=79590\text{ }*1.06 \\ =84365.4 \end{gathered}`

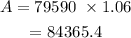
For the fourth year

P=84365.4 + 25000=109365.4

`\begin{gathered} A=\text{ 109365.4}*1.06 \\ =115927.324 \end{gathered}`

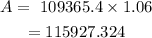
For the fifth year

P= 115927.324 + 25000 =140927.324

`\begin{gathered} A=\text{ 140927.324}*1.06 \\ =149382.962 \end{gathered}`

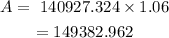
At the start of the 6th year

P= 149382.962+25000= 174382.96

Answer = $174382.96

Option B is correct