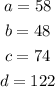Solution:
Given the figure below:
To solve for the missing angles,
Step 1: Solve for c.
The sum of the interior angles of a triangle equals 180 degrees.
Thus,
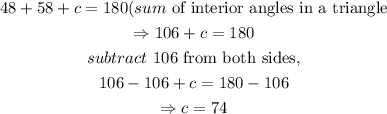
Step 2: Solve for d.
The sum of angles on a straight line gives 180 degrees.
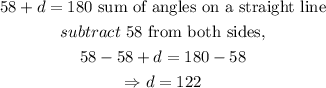
Step 3: Solve for a.
From the figure,
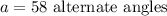
Step 4: Solve for b.
From the figure,
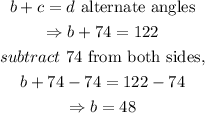
Hence, we have