Question

Is the relationship between the X and Y values in the table below linear, exponential, or neither

Answer 1

The correct option is exponential

Steps

Let's check if the data is linear. Recall that the general form for a linear equation is:

`\begin{gathered} y\text{ = mx + c} \\ \text{where m = }(\Delta y)/(\Delta x) \end{gathered}`

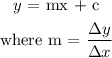
Since the slope should be constant, we can check across two data points.

Using points (3, 48) and (4, 12). The slope(m) is:

`\begin{gathered} m\text{ = }\frac{12\text{ - 48}}{4\text{ -3}} \\ =\text{ -36} \end{gathered}`

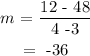
Using the points (4,12) and (5, 3). The slope(m) is :

`\begin{gathered} m\text{ = }\frac{3\text{ - 12}}{5-4} \\ =\text{ -9} \end{gathered}`

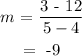
Since, the slope is inconsistent, the table is not linear

To check if it is exponential,

Recall that the general equation for an exponential function is :

`y=a^x`

Using the data points (3,48) and (4,12), we can solve for the constant a, and then check if it is the same across the table.

`\begin{gathered} 48=a^3\text{ } \\ 12=a^4 \\ \text{dividing equation 1 by equation 2} \\ a\text{ = }(1)/(4) \end{gathered}`

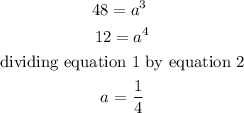
Check:

using points (4,12) and (5,3)

`\begin{gathered} 12=a^4 \\ 3=a^5 \\ \text{dividing equation 2 by 1} \\ a\text{ = }(3)/(12) \\ =\text{ }(1)/(4) \end{gathered}`

Since a is constant across data points, the table represents an exponential equation