The domain of a function is composed of all real numbers for which the function is defined. In the case of a rational expression, such as the given one the function is undefined when its denominator is zero.
Now, solving
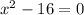
for x we get:
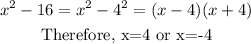
Then, the domain of the function is al real numbers except for 4 and -4.