Question

Assume that 10% of students at a university wear contacts. We randomly pick 200 students. What is the standard deviation of the proportion of students in this group who may wear contacts? Round to 2 decimal places

Answer 1

So we know that the 10% of students at a university wear contacts. This percentage is the proportion of success in the population where a success indicates a student wearing contacts and the total population is made of all the students in the university. In order to make calculations we can write that percentage as fraction by dividing it by 100:

`P=(10)/(100)=0.1`

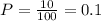
Where I used P to label the proportion described. If we randomly pick a sample of 200 students then the proportion of students in this who wear contacts is a quantity p that not necessarily is equal to P. However, its standard deviation does depends on the value of P. Using the letter sigma for the standard deviation of this sample this is given by the following formula:

`\sigma_p=\sqrt[]{(P\cdot Q)/(n)}`

Where n is the sample size, in this case 200, and Q is the proportion of students at the university that don't wear contacts. Since we have only two possible scenarios: a student wears contacts or doesn't, then the sum of Q and P must be equal to 1 (or 100%):

`\begin{gathered} P+Q=1 \\ Q=1-P \end{gathered}`

Then the standard deviation is given by:

`\sigma_p=\sqrt[]{(P\cdot(1-P))/(n)}=\sqrt[]{(0.1\cdot(1-0.1))/(200)}=\sqrt[]{(0.09)/(200)}=\sqrt[]{0.00045}=0.0212`

So the standard deviation as a fraction is 0.0212 but we need to express it as a percentage so we have to multiply it by 100:

`0.0212\cdot100=2.12`

Then the answer is 2.12.