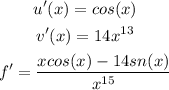Question

Let u(x) = sin(x) and v(x) = x ^ 14 and f(x) = (u(x))/(v(x))

Answer 1

Explanation:

Step 1. We are given the expressions for u(x) and v(x):

`\begin{gathered} u(x)=sin(x) \\ v(x)=x^(14) \end{gathered}`

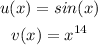
The first two parts of the problem consist of finding the derivative of these two expressions: u'(x) and v'(x).

Step 2. To derivate u(x) we use the following rule:

`\begin{gathered} for\text{ a function } \\ g(x)=sin(x) \\ The\text{ derivative is} \\ g^(\prime)(x)=cos(x) \end{gathered}`

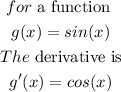
which means that in this case:

`\boxed{u^(\prime)(x)=cos(x)}`

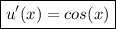
Step 3. To derivate v(x) we use the following rule:

`\begin{gathered} for\text{ a function} \\ g(x)=x^n \\ The\text{ derivative is} \\ g^(\prime)(x)=nx^(n-1) \end{gathered}`

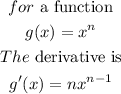
In our case n=14, therefore, the derivative is:

`\begin{gathered} v(x)=x^(14) \\ \downarrow \\ v^(\prime)(x)=14x^(14-1) \end{gathered}`

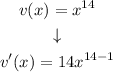
simplifying the exponent:

`\boxed{v^(\prime)(x)=14x^(13)}`

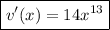
Step 4. Now, to solve the third part of the problem, we consider the definition of f(x) given in the statement:

`f(x)=(u(x))/(v(x))`

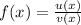
And to find the derivative of this function f'(x) or f', we use the quotient rule,

`f^(\prime)=(u^(\prime)v-uv^(\prime))/(v^2)`

We already know u and v from the given definitions, and we found u' and v' in 2 and 3.

So now, we substitute the known values into the quotient rule formula:

`f^(\prime)=(cos(x)(x^(14))-sin(x)(14x^(13)))/((x^(14))^2)`

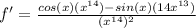
Step 5. The last step is to simplify our result. We start by simplifying the exponent in the denominator:

`f^(\prime)=(cos(x)(x^(14))-s\imaginaryI n(x)(14x^(13)))/(x^(28))`

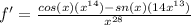
and to simplify further, divide both the numerator and denominator by x^13

`\begin{gathered} f^(\prime)=(cos(x)(x^)-s\imaginaryI n(x)(14))/(x^(15)) \\ \downarrow \\ \boxed{f^(\prime)=(xcos(x)-14sin(x))/(x^(15))} \end{gathered}`

And that is the simplified solution.

Answer:

`\begin{gathered} u^(\prime)(x)=cos(x) \\ v^(\prime)(x)=14x^(13) \\ f^(\prime)=(xcos(x)-14s\imaginaryI n(x))/(x^(15)) \end{gathered}`