Question

A student fires a cannonball vertically upwards with an initial speed v. Determine all unknowns and answer the following questions. Neglect drag and the initial height and horizontal motion of the cannonball. Calculate the maximum height (h) and total flight time (t) in each of the following cases.

Answer 1

This is projectile motion. We know that in this kind of motion the maximum height is given by:

`h_(\max )=(v^2_0\sin \theta)/(2g)`

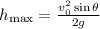
and that, when the motion is complete (this means that the object stops at the same height it begins, like in this case) the total time of flight is given by:

`t=(2v_0\sin \theta)/(g)`

In both of this equations the angle theta represents the angle of launch.

Now, in this case the student fires the cannonball upwards, this means that the angle of launch is 90°; since:

`\sin 90=1`

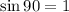
Then, for this problem, the equations above reduced to:

`h_(\max )=(v^2_0)/(2g)`

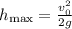
and

`t=(2v_0)/(g)`

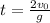
Now that we know this we can plug the initial velocity of each case in the equations above to determine the maximum height and time of flight. For example, if the initial velocity is 13 m/s then we have that:

`\begin{gathered} h_(\max )=(13^2)/(2(9.8))=8.62\text{ m} \\ \text{and} \\ t=(2(13))/(9.8)=2.65\text{ s} \end{gathered}`

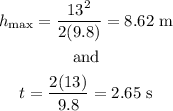
With this procedure we have that the table would be: