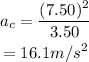Question

The centripetal force acting uptown a 65kg child who makes 12.0 revolutions around the cliffhanger ride in 35.2 seconds. The radius of the barrel is 3.50 meters. Determine vc ac fc

Answer 1

Given data

*The given mass of the child is m = 65 kg

*The given number of revolutions is 12.0

*The given time is t = 35.2 s

*The given radius of the barrel is r = 3.50 m

The frequency is calculated as

`\begin{gathered} f_{}=(12)/(35.0) \\ =0.34\text{ Hz} \end{gathered}`

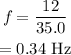
The formula for the linear velocity is given as

`\begin{gathered} v=\omega r \\ =(2\pi f)r \end{gathered}`

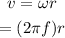
Substitute the known values in the above expression as

`\begin{gathered} v=(2*3.14*0.34)(3.50) \\ =7.47\text{ m/s} \\ \approx7.50\text{ m/s} \end{gathered}`

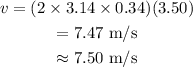
The formula for the centripetal force is given as

`F_c=(mv^2)/(r)`

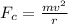
Substitute the known values in the above expression as

`\begin{gathered} F_c=((65)(7.50)^2)/((3.50)) \\ =1045.6\text{ N} \\ =1050\text{ N} \end{gathered}`

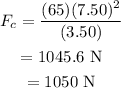
The formula for the centripetal acceleration is given as

`a_c=(v^2)/(r)`

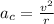
Substitute the known values in the above expression as

`\begin{gathered} a_c=((7.50)^2)/(3.50) \\ =16.1m/s^2 \end{gathered}`