Question

Find the domain of the function expressed by the formulay= 2/3 +xpls write the answer as a equation

Answer 1

The function is

`y=(2)/(3+x)`

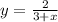
Remember that, for y to be a number, we cannot have things of the form

`\begin{gathered} (1)/(0),(2)/(0),\ldots \\ (1)/(0),(2)/(0),\ldots\\otin\mathfrak{\Re } \end{gathered}`

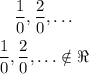
Therefore, we always need to avoid this kind of result.

We can see that the only way 'y' acquires a value like that is if

`\begin{gathered} 3+x=0 \\ \Rightarrow x=-3 \end{gathered}`

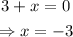
Therefore, y is well for any value of x, except when x=-3.

Thus, the domain of the function y (y(x)) is

`x\in(-\infty,-3)\cup(-3,\infty)=\mathfrak{\Re }-\mleft\lbrace-3\mright\rbrace`

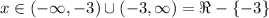
The domain of y is all the numbers except for -3