The hourly wages of employees who work in restaurants in Philadelphia has a normal distribution with mean μ= $5.50 and standard deviation σ=$1.50
The variable of interest X is the hourly wages of one employee who work in restaurants in Philadelphia.
To find the percentiles of the distribution you have to subtract the mean from the determined value of X, and then divide the result by the standard deviation, i.e. you have to find the z-value corresponding to the value of X. Then using the Z-table you have to look for the corresponding proportion.
a) You have to look for the percentile for $7, i.e. the percentage of restaurant employees that have an hourly wage below $7, symbolically:
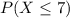
So, the first step is to calculate the z-value as follows:
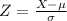
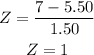
Now what's left is to find the corresponding value in the Z-table

And multiply the probability by 100 to express the decimal value as a percentage:
