To find the slope of a line with two points, we need to find the slope. The slope is defined by the difference between y coordinates divided by the difference between x-coordinates.
For two points A and B:
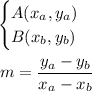
In this case, we can call A(0, 6) and B(7, 2)
Then we calculate:
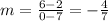
Now that we know the slope, the equation of a line is:
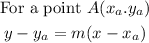
In this case, we know m and we can take A(0, 6):
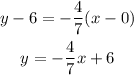
And that's the equation of the line.