Question

Question 22. How could the following equation be factored to find the zeros?

Answer 1

Given the equation:

`y=x^3-3x^2-4x`

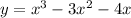
first notice that on the expression on the right, all the terms have at least one common factor x, then, we can write it as follows:

`x^3-3x^2-4x=x(x^2-3x-4)`

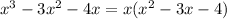
then, the expression that we have between the parenthesis, can be factored as follows:

`x^2-3x-4=(x-4)(x+1)`

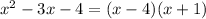
then, the original equation can be factored like this:

`x^3-3x^2-4x=x(x-4)(x+1)`

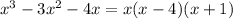
which has zeros x = 0, x = 4 and x = -1