Inverse proportion is when one quantity increases and the other decreases. The two quantities are said to be inversely proportional. The inverse proportion formula is
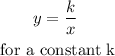
So, in this case, we can write the following equation:
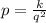
Since we know that the value of p is 18 when q is 2, we can find the value of k:

Now, we can determine the value of p when q is equal to 3:
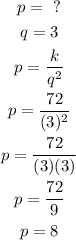
Therefore,