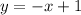We know that two lines are perpendicular if and only if their slopes fullfil:
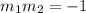
Then we need to find the slope of the equation given:
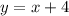
we notice that this equation is written in the slope intercept form:

comparing this equations we notice that:
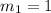
Now, plugging this value in the condition and solving for the second slope we have:
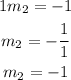
Now that we have the slope of the line we are looking form we plug its value, and the point in the equation:

then:
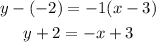
finally we write the equation in the slope intercept form given above:
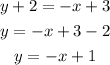
Therefore the equation we are looking for is: